CSC 476/676 AU / Homework 3 / Image Blending Using Pyramids

Figure 1: Blended Image of an Apple and Orange
A Gaussian image pyramid is constructed by blurring, then downsampling an image, and repeating the process on the resulting image until a desired state is achieved. It generates versions of the same image, but with varying resolutions. A Laplacian image pyramid can be generated as a result of a Gaussian image pyramid. Each level of a Laplacian image pyramid is the difference between a level in the Gaussian image pyramid and its blurred image. By subtracting the blurred image from a given level in the Gaussian image pyramid, we end up with only the details of the image of the given level in the Gaussian image pyramid. With the details, one can reconstruct an image using only the most coarse version of the image in a Gaussian image pyramid. In addition, the Laplacian image pyramid, combined with a Gaussian image pyramid allows one to seamlessly blend two images together using a mask as seen in Figure 1.
For the images generated in this particular report (as seen in Figure 2) I blended images of an apple and orange together using the following steps:
- Build Laplacian image pyramids for each image, multiplying each layer with a Gaussian filtered mask to ensure only half of each image was being included in the image pyramid. Add the resulting images in each layer together.
- Build Gaussian image pyramids for each image, and use just the final layer of both pyramids as the starting point of reconstructing a blended image. Same as step 1, multiply both images with a Gaussian filtered mask of the same size to ensure only half of each image remains. Add the resulting images together.
- Add the resulting images from step 1 with the images from step 2. By adding images that include only details of the original image (images from step 1) with smoothed images (images from step 2), we're able to reconstruct the first version of the blended image.
- Upscale and blur (interpolate) the image in step 3, and add the next layer of the Laplacian image pyramid from step 1. This reconstructs the next, more detailed version of the blended image.
- Repeat step 4, interpolating the resulting image and adding the next layer of the Laplacian image pyramid, until all levels of the Laplacian image pyramid are exhausted, at which point the final version of the blended image is generated.
Step by Step Explanation of Code Used To Blend apple.jpg and orange.jpg Together
Import necessary libraries and set the working directory to wherever your images are stored:
#Import libraries and install where necessary
import numpy as np
import scipy.signal as sig
from scipy import misc
import matplotlib.pyplot as plt
from scipy import ndimage
import imageio
import cv2
from PIL import Image
import os
#Replace with your path to where the images are stored
path = '/Users/kojiro/Downloads/homework3/html/'
#Set current working directory to provided path
os.chdir(path)
print(os.getcwd())
#Read provided images
def image_prep(image1, image2, mask):
image1 = imageio.imread(path + image1, as_gray = True)
image2 = imageio.imread(path + image2, as_gray = True)
mask = imageio.imread(path + 'mask.jpg',as_gray = True)
image1 = cv2.resize(image1, (512, 512))
image2 = cv2.resize(image2, (512, 512))
return image1, image2, mask
Code provided by Professor Xiao, which includes interpolate (upsample and blur), decimate (blur and downsample), and pyramids (generates Laplacian and Gaussian pyramids) methods
# create a Binomial (5-tap) filter
kernel = (1.0/256)*np.array([[1, 4, 6, 4, 1],[4, 16, 24, 16, 4],[6, 24, 36, 24, 6],[4, 16, 24, 16, 4],[1, 4, 6, 4, 1]])
def interpolate(image):
"""
Interpolates an image with upsampling rate r=2.
"""
image_up = np.zeros((2*image.shape[0], 2*image.shape[1]))
# Upsample
image_up[::2, ::2] = image
# Blur (we need to scale this up since the kernel has unit area)
# (The length and width are both doubled, so the area is quadrupled)
#return sig.convolve2d(image_up, 4*kernel, 'same')
return ndimage.filters.convolve(image_up,4*kernel, mode='constant')
def decimate(image):
"""
Decimates at image with downsampling rate r=2.
"""
# Blur
#image_blur = sig.convolve2d(image, kernel, 'same')
image_blur = ndimage.filters.convolve(image,kernel, mode='constant')
# Downsample
return image_blur[::2, ::2]
def pyramids(image):
"""
Constructs Gaussian and Laplacian pyramids.
Parameters :
image : the original image (i.e. base of the pyramid)
Returns :
G : the Gaussian pyramid
L : the Laplacian pyramid
"""
# Initialize pyramids
G = [image, ]
L = []
# Build the Gaussian pyramid to maximum depth
while image.shape[0] >= 2 and image.shape[1] >= 2:
image = decimate(image)
G.append(image)
# Build the Laplacian pyramid
for i in range(len(G) - 1):
L.append(G[i] - interpolate(G[i + 1]))
return G[:-1], L
def reconstruct(L,G):
rows, cols = img.shape
composite_image = np.zeros((rows, cols + cols / 2), dtype=np.double)
composite_image[:rows, :cols] = G[0]
i_row = 0
for p in G[1:]:
n_rows, n_cols = p.shape[:2]
composite_image[i_row:i_row + n_rows, cols:cols + n_cols] = p
i_row += n_rows
fig, ax = plt.subplots()
ax.imshow(composite_image,cmap='gray')
plt.show()
rows, cols = img.shape
composite_image = np.zeros((rows, cols + cols / 2), dtype=np.double)
composite_image[:rows, :cols] = L[0]
i_row = 0
for p in L[1:]:
n_rows, n_cols = p.shape[:2]
composite_image[i_row:i_row + n_rows, cols:cols + n_cols] = p
i_row += n_rows
fig, ax = plt.subplots()
ax.imshow(composite_image,cmap='gray')
plt.show()
Generate Laplacian and Gaussian image pyramids for both the apple and orange images, as well as a Gaussian image pyramid for the mask for both the apple and orange images
def laplacian_pyramid(image, bools = False):
laplacian_pyramid = pyramids(image)[1]
fig, ax = plt.subplots(1, 9, figsize = (20,20))
for i in range(len(laplacian_pyramid)):
ax[i].imshow(laplacian_pyramid[i], cmap = 'gray')
i = 0
while os.path.exists('{}{:d}.jpg'.format('laplacian_pyramid', i)):
i += 1
if bools == True:
fig.savefig('{}{:d}.jpg'.format('laplacian_pyramid', i), bbox_inches='tight')
plt.close()
return laplacian_pyramid
def gaussian_pyramid(image, bools = False):
gaussian_pyramid = pyramids(image)[0]
fig, ax = plt.subplots(1, 9, figsize = (20,20))
for i in range(len(gaussian_pyramid)):
ax[i].imshow(gaussian_pyramid[i], cmap = 'gray')
i = 0
while os.path.exists('{}{:d}.jpg'.format('gaussian_pyramid', i)):
i += 1
if bools == True:
fig.savefig('{}{:d}.jpg'.format('gaussian_pyramid', i), bbox_inches='tight')
plt.close()
return gaussian_pyramid
def gaussian_mask(mask, bools = False):
gaussian_pyramid_mask = pyramids(mask)[0]
fig, ax = plt.subplots(1, 9, figsize = (20,20))
for i in range(len(gaussian_pyramid_mask)):
ax[i].imshow(gaussian_pyramid_mask[i], cmap = 'gray')
if bools == True:
fig.savefig('gaussian_pyramid_mask.jpg', bbox_inches='tight')
plt.close()
return gaussian_pyramid_mask
def gaussian_mask_inverted(mask, bools = False):
flipped = np.flip(mask)
gaussian_pyramid_mask_inverted = pyramids(flipped)[0]
fig, ax = plt.subplots(1, 9, figsize = (20,20))
for i in range(len(gaussian_pyramid_mask_inverted)):
ax[i].imshow(gaussian_pyramid_mask_inverted[i], cmap = 'gray')
if bools == True:
fig.savefig('gaussian_pyramid_mask_inverted.jpg', bbox_inches='tight')
plt.close()
return gaussian_pyramid_mask_inverted
Combine the Laplacian image levels of each pyramid. Also combine the lowest level of the Gaussian image pyramid for each image.
def merge_laplacians(laplacian_pyramid_image1, laplacian_pyramid_image2, gaussian_mask_image1, gaussian_mask_image2):
#Combine each laplacian level (masked) of each pyramid
#(i.e. each level of laplacian_pyramid_orange + laplacian_pyramid_apple)
combined_laplacian = []
for i in range(-2, -len(laplacian_pyramid_image1)-1, -1):
lap_image1 = laplacian_pyramid_image1[i] * gaussian_mask_image1[i]
lap_image2 = laplacian_pyramid_image2[i] * gaussian_mask_image2[i]
combined_laplacian.append(lap_image1 + lap_image2)
return combined_laplacian
def merge_gaussians(gaussian_pyramid_image1, gaussian_pyramid_image2, gaussian_mask_image1, gaussian_mask_image2):
#Combine lowest gaussian level (masked) of each pyramid
gaus_image1 = interpolate(gaussian_pyramid_image1[-1]) * gaussian_mask_image1[-2]
gaus_image2 = interpolate(gaussian_pyramid_image2[-1]) * gaussian_mask_image2[-2]
combined_gaussian = gaus_image1 + gaus_image2
return combined_gaussian
Finally, blend the two images together. This is achieved by adding each level of the combined Laplacian image pyramid, initially with the combined lowest level of the Gaussian image pyramid, then the resulting image for the remaining iterations.
def blend(merged_laplacian_result, merged_gaussian_result, bools = False):
#Blend orange and apple together
blended = merged_laplacian_result[0] + merged_gaussian_result
blended_final = blended
for i in range(1, 8):
blended_final = interpolate(blended_final) + merged_laplacian_result[i]
fig, ax = plt.subplots(1,1, figsize = (5,5))
ax.imshow(blended_final, cmap = 'gray')
i = 0
while os.path.exists('{}{:d}.jpg'.format('blended_final', i)):
i += 1
if bools == True:
fig.savefig('{}{:d}.jpg'.format('blended_final', i), bbox_inches='tight')
plt.close()
return blended_final
def reconstruct_channels(blended, rotate = False):
#Reconstruct channels and stack in color channels
stacked_img = np.stack((blended, )*3, axis = -1)
stacked_img = stacked_img/np.amax(stacked_img)
if rotate == True:
stacked_img = np.rot90(stacked_img, k = 3)
fig, ax = plt.subplots(1,1, figsize = (5,5))
ax.imshow(stacked_img, cmap ='gray')
i = 0
while os.path.exists('{}{:d}.jpg'.format('final_image', i)):
i += 1
fig.savefig('{}{:d}.jpg'.format('final_image', i), bbox_inches='tight')
plt.close()
return stacked_img
def blend_images(image1, image2, mask, bools = False, rotate = False):
#Running all methods
image1, image2, mask = image_prep(image1, image2, mask)
laplacian_image1 = laplacian_pyramid(image1, bools)
laplacian_image2 = laplacian_pyramid(image2, bools)
gaussian_image1 = gaussian_pyramid(image1, bools)
gaussian_image2 = gaussian_pyramid(image2, bools)
image1_mask = gaussian_mask(mask, bools)
image2_mask = gaussian_mask_inverted(mask, bools)
merged_laplacian = merge_laplacians(laplacian_image1, laplacian_image2, image1_mask, image2_mask)
merged_gaussian = merge_gaussians(gaussian_image1, gaussian_image2, image1_mask, image2_mask)
blended_image = blend(merged_laplacian, merged_gaussian, bools)
final_image = reconstruct_channels(blended_image, rotate)
apple_orange = blend_images('orange.jpg', 'apple.jpg','mask.jpg', bools = True)
centaur = blend_images('man_crawling.png', 'horse_up.png', 'mask.jpg')
dog_portrait = blend_images('Picture2.jpg', 'Picture1.jpg', 'mask.jpg')
sun_flower = blend_images('sun.png', 'flower.png', 'mask.jpg')
falling_woman = blend_images('water.png', 'falling2.png', 'mask.jpg', rotate = True)
Figure 2: Plots of Intermediary Steps and Final Image

|

|

|

|

|

|

With Recovered RGB Channels 
|
For the provided images (apple.jpg and orange.jpg), the algorithm I used seem to work well. The apple and orange are blended together fairly seamlessly, although one could argue that a variation on this algorithm that further obfuscates the blending point between the orange and the apple might provide a more realistic or believable result. Compared to other implementations of this process (as seen documented here "Image Pyramids " by OpenCV, and documented here "Image Blending Using Laplacian Pyramids" (Zhao, 2020)), the result of my algorithm holds up against both of these implementations, with the exception of recoloring the image possibly proving otherwise.
In addition to the frequently used apple.jpg and orange.jpg, I also applied the algorithm to other images to see how it performs and whether the resulting image can still be considered 'natural'.
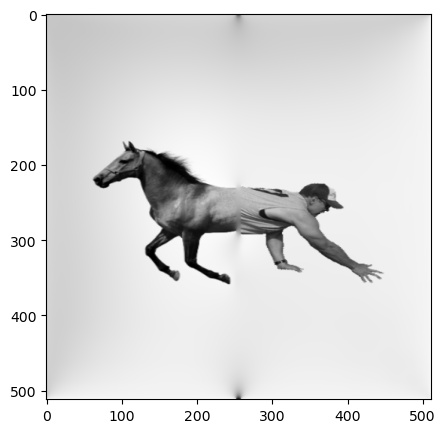
The first of these attempts titled "Horse and Man" seemed to work somewhat successfully. While the image looks mostly 'natural', the difference in texture between the man's shirt and the horse's skin leaves room for improvement.
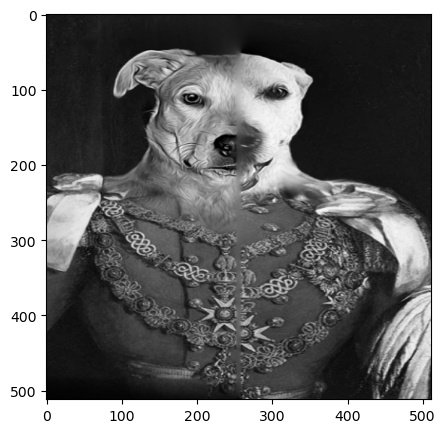
In Figure 4, I combined two portrait images of two different dogs. The resulting image looks slightly awakard due to mismatching details such as parts of their clothes not lining up and their unaligned eye lines. This is a good example in which the algoirthm works poorly, caused by the high level of detail in the two original images.
In Figure 5, I blended an image of a flower and an image of the sun. This worked well because both images were symmetrical, and both also had overall similar shapes. The rays from the circular sun, and the petals stemming from the circular bud resulted in a seamless blend of the two images.

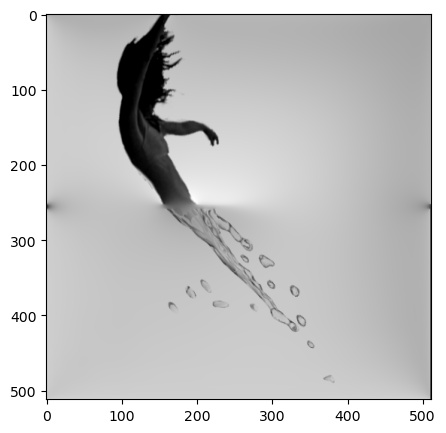
Finallly, in Figure 6, the algorithm succeeded in blending an image of a woman and a splash of water. This worked surprisngly well despite the contrasting textures, perhaps due to the two images aligning in a 'natural' way that seems believeable, in that the water spalash looks somewhat like the woman's legs. This image was rotated vertically after blending.
Citations
Grizzlybear.se. (2017). [Sun in Blue Sky][Photograph]. https://flic.kr/p/Vck8cv
Image pyramids. OpenCV. (n.d.). Retrieved November 15, 2021, from https://docs.opencv.org/4.x/dc/dff/ tutorial_py_pyramids.html.
[Man Bear Crawling]. (n.d.). Constant Fitness. https://www.constantfitness.com/public/187.cfm
[Purple Flower]. (n.d.). NICEPNG. https://www.nicepng.com/ourpic/u2q8a9w7w7e
RenaissancePet. (n.d.). [Brown Dog Portrait][Digital]. Etsy. https://www.etsy.com/listing/210123053/prince-albert-custom-pet-portraits-dog
RenaissancePet. (n.d.). [White Dog Portrait][Digital]. Etsy. https://www.etsy.com/listing/210123053/prince-albert-custom-pet-portraits-dog
[Silhouette of Woman Falling]. (n.d.). VHV. https://www.vhv.rs/viewpic/hRJJRRm_ftestickers-people-woman-falling-silhoutte-danial8986-silhouette-of/
Wall, Abjsabar. (2019). [horse png PNG image with transparent background][Photograph]. toppng. https://toppng.com/horse-png-PNG-free-PNG-Images_121020
[Water Drop Splash]. (n.d.). PNGITEM. https://www.pngitem.com/middle/hJJmTwJ_water-drop-splash-png-transparent-png/
Zhao, M. (2020, May 14). Image blending using Laplacian pyramids. Medium. Retrieved November 21, 2021, from https://becominghuman.ai/image-blending-using-laplacian-pyramids-2f8e9982077f.