Kojiro So

Figure 1: Blended Image of an Apple and Orange

Step by Step Explanation of Code Used To Blend apple.jpg and orange.jpg Together

Import necessary libraries and set the working directory to wherever your images are stored:

#Import libraries and install where necessary
import numpy as np
import scipy.signal as sig
from scipy import misc
import matplotlib.pyplot as plt
from scipy import ndimage
import imageio
import cv2
from PIL import Image
import os

#Replace with your path to where the images are stored
path = '/Users/kojiro/Downloads/homework3/html/'
#Set current working directory to provided path
os.chdir(path)
print(os.getcwd())

#Read provided images
def image_prep(image1, image2, mask):
  image1 = imageio.imread(path + image1, as_gray = True)
  image2 = imageio.imread(path + image2, as_gray = True)
  mask = imageio.imread(path + 'mask.jpg',as_gray = True)
  image1 = cv2.resize(image1, (512, 512))
  image2 = cv2.resize(image2, (512, 512))
  return image1, image2, mask

Code provided by Professor Xiao, which includes interpolate (upsample and blur), decimate (blur and downsample), and pyramids (generates Laplacian and Gaussian pyramids) methods

# create a  Binomial (5-tap) filter
kernel = (1.0/256)*np.array([[1, 4,  6,  4,  1],[4, 16, 24, 16, 4],[6, 24, 36, 24, 6],[4, 16, 24, 16, 4],[1, 4,  6,  4,  1]])

def interpolate(image):
    """
    Interpolates an image with upsampling rate r=2.
    """
    image_up = np.zeros((2*image.shape[0], 2*image.shape[1]))
    # Upsample
    image_up[::2, ::2] = image
    # Blur (we need to scale this up since the kernel has unit area)
    # (The length and width are both doubled, so the area is quadrupled)
    #return sig.convolve2d(image_up, 4*kernel, 'same')
    return ndimage.filters.convolve(image_up,4*kernel, mode='constant')
                                
def decimate(image):
    """
    Decimates at image with downsampling rate r=2.
    """
    # Blur
    #image_blur = sig.convolve2d(image, kernel, 'same')
    image_blur = ndimage.filters.convolve(image,kernel, mode='constant')
    # Downsample
    return image_blur[::2, ::2]                                
                                                        
def pyramids(image):
    """
    Constructs Gaussian and Laplacian pyramids.
    Parameters :
        image  : the original image (i.e. base of the pyramid)
    Returns :
        G   : the Gaussian pyramid
        L   : the Laplacian pyramid
    """
    # Initialize pyramids
    G = [image, ]
    L = []

    # Build the Gaussian pyramid to maximum depth
    while image.shape[0] >= 2 and image.shape[1] >= 2:
        image = decimate(image)
        G.append(image)
        
    # Build the Laplacian pyramid
    for i in range(len(G) - 1):
        L.append(G[i] - interpolate(G[i + 1]))

    return G[:-1], L

def reconstruct(L,G):
  rows, cols = img.shape
  composite_image = np.zeros((rows, cols + cols / 2), dtype=np.double)
  composite_image[:rows, :cols] = G[0]

  i_row = 0
  for p in G[1:]:
      n_rows, n_cols = p.shape[:2]
      composite_image[i_row:i_row + n_rows, cols:cols + n_cols] = p
      i_row += n_rows


  fig, ax = plt.subplots()
      
  ax.imshow(composite_image,cmap='gray')
  plt.show()


  rows, cols = img.shape
  composite_image = np.zeros((rows, cols + cols / 2), dtype=np.double)

  composite_image[:rows, :cols] = L[0]

  i_row = 0
  for p in L[1:]:
      n_rows, n_cols = p.shape[:2]
      composite_image[i_row:i_row + n_rows, cols:cols + n_cols] = p
      i_row += n_rows


  fig, ax = plt.subplots()
    
  ax.imshow(composite_image,cmap='gray')
  plt.show()

Generate Laplacian and Gaussian image pyramids for both the apple and orange images, as well as a Gaussian image pyramid for the mask for both the apple and orange images

def laplacian_pyramid(image, bools = False):
  laplacian_pyramid = pyramids(image)[1]
  fig, ax = plt.subplots(1, 9, figsize = (20,20))
  for i in range(len(laplacian_pyramid)):
    ax[i].imshow(laplacian_pyramid[i], cmap = 'gray')
  i = 0
  while os.path.exists('{}{:d}.jpg'.format('laplacian_pyramid', i)):
    i += 1
  if bools == True:    
    fig.savefig('{}{:d}.jpg'.format('laplacian_pyramid', i), bbox_inches='tight')
  plt.close()  
  return laplacian_pyramid

def gaussian_pyramid(image, bools = False):
  gaussian_pyramid = pyramids(image)[0]
  fig, ax = plt.subplots(1, 9, figsize = (20,20))
  for i in range(len(gaussian_pyramid)):
    ax[i].imshow(gaussian_pyramid[i], cmap = 'gray')
  i = 0
  while os.path.exists('{}{:d}.jpg'.format('gaussian_pyramid', i)):
    i += 1
  if bools == True:    
    fig.savefig('{}{:d}.jpg'.format('gaussian_pyramid', i), bbox_inches='tight')
  plt.close()  
  return gaussian_pyramid

def gaussian_mask(mask, bools = False):
  gaussian_pyramid_mask = pyramids(mask)[0]
  fig, ax = plt.subplots(1, 9, figsize = (20,20))
  for i in range(len(gaussian_pyramid_mask)):
    ax[i].imshow(gaussian_pyramid_mask[i], cmap = 'gray')
  if bools == True:  
    fig.savefig('gaussian_pyramid_mask.jpg', bbox_inches='tight')
  plt.close()  
  return gaussian_pyramid_mask

def gaussian_mask_inverted(mask, bools = False):
  flipped = np.flip(mask)
  gaussian_pyramid_mask_inverted = pyramids(flipped)[0]
  fig, ax = plt.subplots(1, 9, figsize = (20,20))
  for i in range(len(gaussian_pyramid_mask_inverted)):
    ax[i].imshow(gaussian_pyramid_mask_inverted[i], cmap = 'gray')  
  if bools == True:
    fig.savefig('gaussian_pyramid_mask_inverted.jpg', bbox_inches='tight')
  plt.close()  
  return gaussian_pyramid_mask_inverted

Combine the Laplacian image levels of each pyramid. Also combine the lowest level of the Gaussian image pyramid for each image.

def merge_laplacians(laplacian_pyramid_image1, laplacian_pyramid_image2, gaussian_mask_image1, gaussian_mask_image2):
  #Combine each laplacian level (masked) of each pyramid 
  #(i.e. each level of laplacian_pyramid_orange + laplacian_pyramid_apple)
  combined_laplacian = []
  for i in range(-2, -len(laplacian_pyramid_image1)-1, -1):
    lap_image1 = laplacian_pyramid_image1[i] * gaussian_mask_image1[i]
    lap_image2 = laplacian_pyramid_image2[i] * gaussian_mask_image2[i]
    combined_laplacian.append(lap_image1 + lap_image2)  
  return combined_laplacian

def merge_gaussians(gaussian_pyramid_image1, gaussian_pyramid_image2, gaussian_mask_image1, gaussian_mask_image2):
  #Combine lowest gaussian level (masked) of each pyramid
  gaus_image1 = interpolate(gaussian_pyramid_image1[-1]) * gaussian_mask_image1[-2]
  gaus_image2 = interpolate(gaussian_pyramid_image2[-1]) * gaussian_mask_image2[-2]
  combined_gaussian = gaus_image1 + gaus_image2
  return combined_gaussian

Finally, blend the two images together. This is achieved by adding each level of the combined Laplacian image pyramid, initially with the combined lowest level of the Gaussian image pyramid, then the resulting image for the remaining iterations.

def blend(merged_laplacian_result, merged_gaussian_result, bools = False):
  #Blend orange and apple together
  blended = merged_laplacian_result[0] + merged_gaussian_result
  blended_final = blended
  for i in range(1, 8):
    blended_final = interpolate(blended_final) + merged_laplacian_result[i]
  fig, ax = plt.subplots(1,1, figsize = (5,5))
  ax.imshow(blended_final, cmap = 'gray')
  i = 0
  while os.path.exists('{}{:d}.jpg'.format('blended_final', i)):
    i += 1
  if bools == True:    
    fig.savefig('{}{:d}.jpg'.format('blended_final', i), bbox_inches='tight')
  plt.close()  
  return blended_final

def reconstruct_channels(blended, rotate = False):
  #Reconstruct channels and stack in color channels
  stacked_img = np.stack((blended, )*3, axis = -1)
  stacked_img = stacked_img/np.amax(stacked_img)
  if rotate == True:
    stacked_img = np.rot90(stacked_img, k = 3)
  fig, ax = plt.subplots(1,1, figsize = (5,5))
  ax.imshow(stacked_img, cmap ='gray')
  i = 0
  while os.path.exists('{}{:d}.jpg'.format('final_image', i)):
    i += 1
  fig.savefig('{}{:d}.jpg'.format('final_image', i), bbox_inches='tight')
  plt.close()
  return stacked_img

def blend_images(image1, image2, mask, bools = False, rotate = False):
  #Running all methods
  image1, image2, mask = image_prep(image1, image2, mask)
  laplacian_image1 = laplacian_pyramid(image1, bools)
  laplacian_image2 = laplacian_pyramid(image2, bools)
  gaussian_image1 = gaussian_pyramid(image1, bools)
  gaussian_image2 = gaussian_pyramid(image2, bools)
  image1_mask = gaussian_mask(mask, bools)
  image2_mask = gaussian_mask_inverted(mask, bools)
  merged_laplacian = merge_laplacians(laplacian_image1, laplacian_image2, image1_mask, image2_mask)
  merged_gaussian = merge_gaussians(gaussian_image1, gaussian_image2, image1_mask, image2_mask)
  blended_image = blend(merged_laplacian, merged_gaussian, bools)
  final_image = reconstruct_channels(blended_image, rotate)	

apple_orange = blend_images('orange.jpg', 'apple.jpg','mask.jpg', bools = True)
centaur = blend_images('man_crawling.png', 'horse_up.png', 'mask.jpg')
dog_portrait = blend_images('Picture2.jpg', 'Picture1.jpg', 'mask.jpg')
sun_flower = blend_images('sun.png', 'flower.png', 'mask.jpg')
falling_woman = blend_images('water.png', 'falling2.png', 'mask.jpg', rotate = True)

Figure 2: Plots of Intermediary Steps and Final Image

For the provided images (apple.jpg and orange.jpg), the algorithm I used seem to work well. The apple and orange are blended together fairly seamlessly, although one could argue that a variation on this algorithm that further obfuscates the blending point between the orange and the apple might provide a more realistic or believable result. Compared to other implementations of this process (as seen documented here "Image Pyramids " by OpenCV, and documented here "Image Blending Using Laplacian Pyramids" (Zhao, 2020)), the result of my algorithm holds up against both of these implementations, with the exception of recoloring the image possibly proving otherwise.

In addition to the frequently used apple.jpg and orange.jpg, I also applied the algorithm to other images to see how it performs and whether the resulting image can still be considered 'natural'.

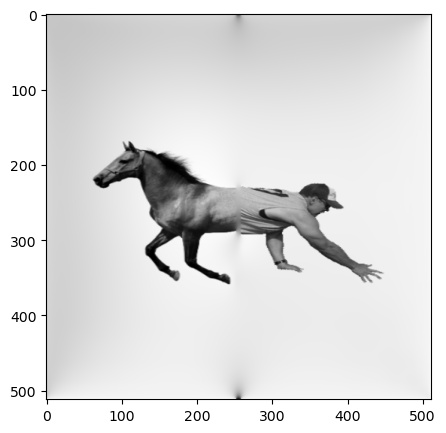
The first of these attempts titled "Horse and Man" seemed to work somewhat successfully. While the image looks mostly 'natural', the difference in texture between the man's shirt and the horse's skin leaves room for improvement.

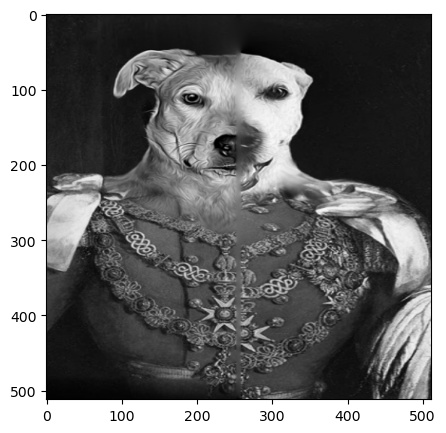
In Figure 4, I combined two portrait images of two different dogs. The resulting image looks slightly awakard due to mismatching details such as parts of their clothes not lining up and their unaligned eye lines. This is a good example in which the algoirthm works poorly, caused by the high level of detail in the two original images.

In Figure 5, I blended an image of a flower and an image of the sun. This worked well because both images were symmetrical, and both also had overall similar shapes. The rays from the circular sun, and the petals stemming from the circular bud resulted in a seamless blend of the two images.

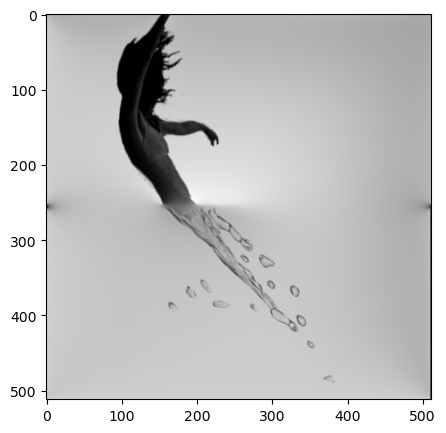
Finallly, in Figure 6, the algorithm succeeded in blending an image of a woman and a splash of water. This worked surprisngly well despite the contrasting textures, perhaps due to the two images aligning in a 'natural' way that seems believeable, in that the water spalash looks somewhat like the woman's legs. This image was rotated vertically after blending.

Citations

Grizzlybear.se. (2017). [Sun in Blue Sky][Photograph]. https://flic.kr/p/Vck8cv

Image pyramids. OpenCV. (n.d.). Retrieved November 15, 2021, from https://docs.opencv.org/4.x/dc/dff/ tutorial_py_pyramids.html.

[Man Bear Crawling]. (n.d.). Constant Fitness. https://www.constantfitness.com/public/187.cfm

[Purple Flower]. (n.d.). NICEPNG. https://www.nicepng.com/ourpic/u2q8a9w7w7e

RenaissancePet. (n.d.). [Brown Dog Portrait][Digital]. Etsy. https://www.etsy.com/listing/210123053/prince-albert-custom-pet-portraits-dog

RenaissancePet. (n.d.). [White Dog Portrait][Digital]. Etsy. https://www.etsy.com/listing/210123053/prince-albert-custom-pet-portraits-dog

[Silhouette of Woman Falling]. (n.d.). VHV. https://www.vhv.rs/viewpic/hRJJRRm_ftestickers-people-woman-falling-silhoutte-danial8986-silhouette-of/

Wall, Abjsabar. (2019). [horse png PNG image with transparent background][Photograph]. toppng. https://toppng.com/horse-png-PNG-free-PNG-Images_121020

[Water Drop Splash]. (n.d.). PNGITEM. https://www.pngitem.com/middle/hJJmTwJ_water-drop-splash-png-transparent-png/

Zhao, M. (2020, May 14). Image blending using Laplacian pyramids. Medium. Retrieved November 21, 2021, from https://becominghuman.ai/image-blending-using-laplacian-pyramids-2f8e9982077f.